Translation, Reposition, Rotation.
Hello and welcome to my 6th weekly check-in. The first evaluation period officially ends and I am very excited to move on to the second coding period. I will be sharing my progress with handling specific object's properties among various multiple objects rendered by a single actor. I am mainly focusing on making it easier to translate, rotate and reposition a particular object, so that I can use them to render physics simulations more efficiently. The official repository of my sub-org, FURY can always be found here.
What did you do this week?
Last week I worked on physics simulations rendered in FURY with the help of pyBullet. Now the simulations were highly un-optimized, specially the brick wall simulation as each brick was rendered by its own actor. In other words, 1 brick = 1 actor. Now my objective was to render all the bricks using a single actor, but before jumping into the simulation I had to figure out how to modify specific properties of an individual object. Thanks to my mentor's PR, I was able to experiment my implementations quickly.
Translation:
The algorithm behind translation is to first identify the vertices of the object, then bring the vertices to the origin by subtracting their centers and then adding the displacement vector. The said operation can be achieved by the following snippet:
# Update vertices positions
vertices[object_index * sec: object_index * sec + sec] = \
(vertices[object_index * sec: object_index * sec + sec] -
centers[object_index]) + transln_vectorRotation:
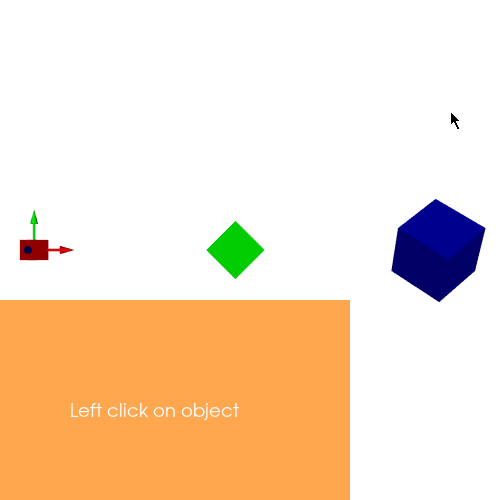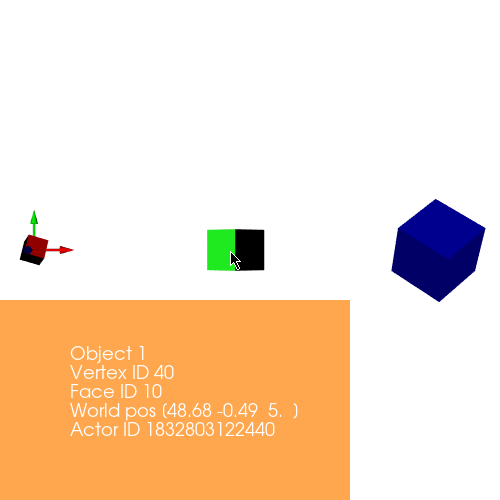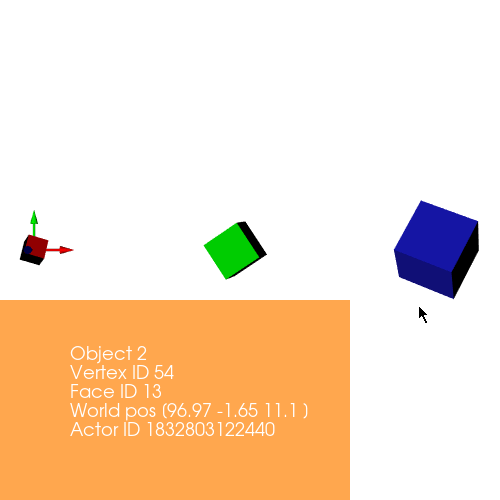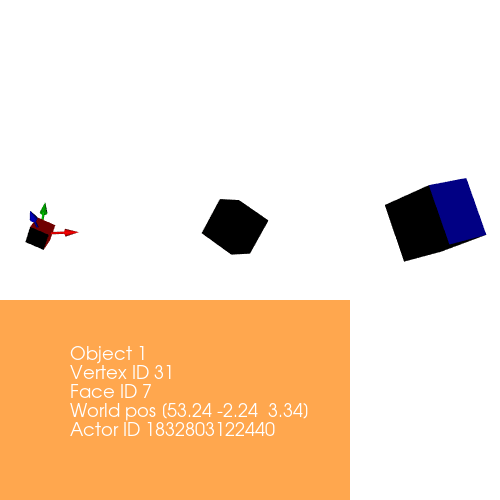
The algorithm behind rotation is to first calculate the difference between the vertices and the center of the object. Once we get the resultant matrix, we matrix multiply it with the rotation matrix and then we further add the centers back to it so that we preserve the position of the object. Rotation matrix can be defined as:
where gamma, beta and alpha corresponds to the angle of rotation along Z-axis, Y-axis and X-axis.
def get_R(gamma, beta, alpha):
""" Returns rotational matrix.
"""
r = [
[np.cos(alpha)*np.cos(beta), np.cos(alpha)*np.sin(beta)*np.sin(gamma) - np.sin(alpha)*np.cos(gamma),
np.cos(alpha)*np.sin(beta)*np.cos(gamma) + np.sin(alpha)*np.sin(gamma)],
[np.sin(alpha)*np.cos(beta), np.sin(alpha)*np.sin(beta)*np.sin(gamma) + np.cos(alpha)*np.cos(gamma),
np.sin(alpha)*np.sin(beta)*np.cos(gamma) - np.cos(alpha)*np.sin(gamma)],
[-np.sin(beta), np.cos(beta)*np.sin(gamma), np.cos(beta)*np.cos(gamma)]
]
r = np.array(r)
return r
vertices[object_index * sec: object_index * sec + sec] = \
(vertices[object_index * sec: object_index * sec + sec] -
centers[object_index])@get_R(0, np.pi/4, np.pi/4) + centers[object_index]Reposition:
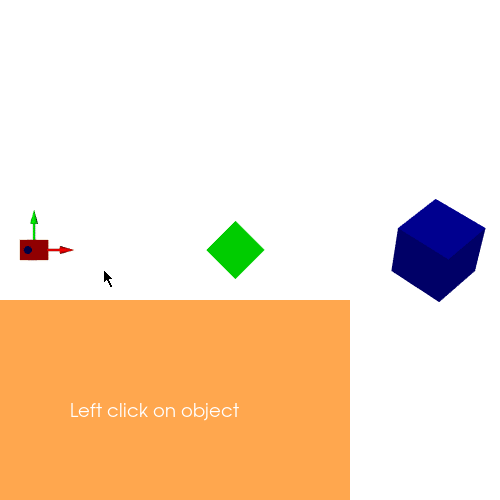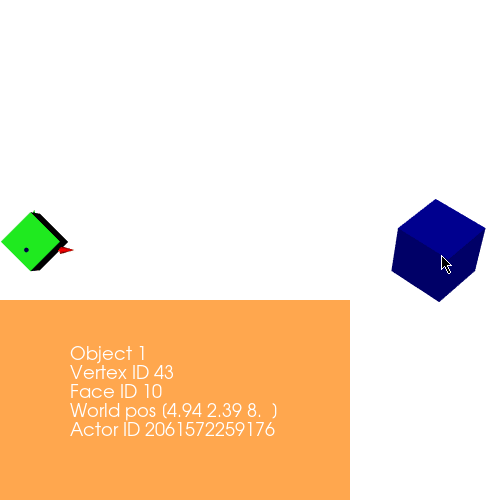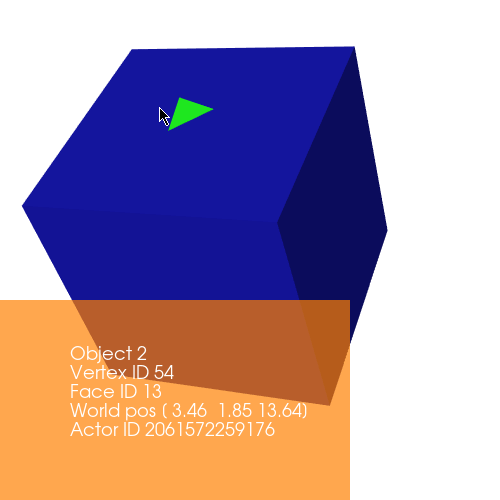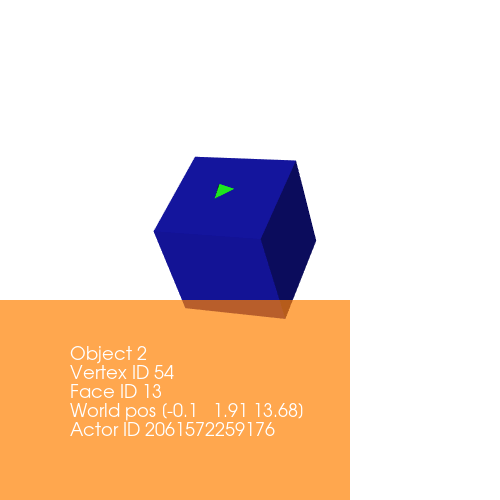
Repositioning is similar to that of translation, except in this case, while repositioning we update centers with the new position value.
new_pos = np.array([1, 2, 3])
# Update vertices positions
vertices[object_index * sec: object_index * sec + sec] = \
(vertices[object_index * sec: object_index * sec + sec] -
centers[object_index]) + new_pos
centers[object_index] = new_posWhat is coming up next?
Currently, I am yet to figure out the orientation problem. Once I figure that out I will be ready to implement simulations without any major issues. I am also tasked with creating a wrecking ball simulation and a quadruped robot simulation.
Did you get stuck anywhere?
I did face some problems while rotating objects. My mentors suggested me to implement it via rotation matrix. I still haven't figured out the orientation problem, which I plan to work on next. Apart from these I did not face any major issues.
