Google Summer of Code 2023 Final Work Product
- Name: Tania Castillo
- Organisation: Python Software Foundation
- Sub-Organisation: FURY
- Project: SDF-based uncertainty representation for dMRI glyphs
Abstract
Diffusion Magnetic Resonance Imaging (dMRI) is a non-invasive imaging technique used by neuroscientists to measure the diffusion of water molecules in biological tissue. The directional information is reconstructed using either a Diffusion Tensor Imaging (DTI) or High Angular Resolution Diffusion Imaging (HARDI) based model, which is graphically represented as tensors and Orientation Distribution Functions (ODF). Traditional rendering engines discretize Tensor and ODF surfaces using triangles or quadrilateral polygons, making their visual quality depending on the number of polygons used to build the 3D mesh, which might compromise real-time display performance. This project proposes a methodological approach to further improve the visualization of DTI tensors and HARDI ODFs glyphs by using well-established techniques in the field of computer graphics, such as geometry amplification, billboarding, signed distance functions (SDFs), and ray marching.
Proposed Objectives
- Implement a parallelized version of computer-generated billboards using geometry shaders for amplification.
- Model the mathematical functions that express the geometry of ellipsoid glyphs and implement them using Ray Marching techniques.
- Model the mathematical functions that express the geometry of ODF glyphs and implement them using Ray Marching techniques.
- Use SDF properties and techniques to represent the uncertainty of dMRI reconstruction models.
Objectives Completed
-
Ellipsoid actor implemented with SDF
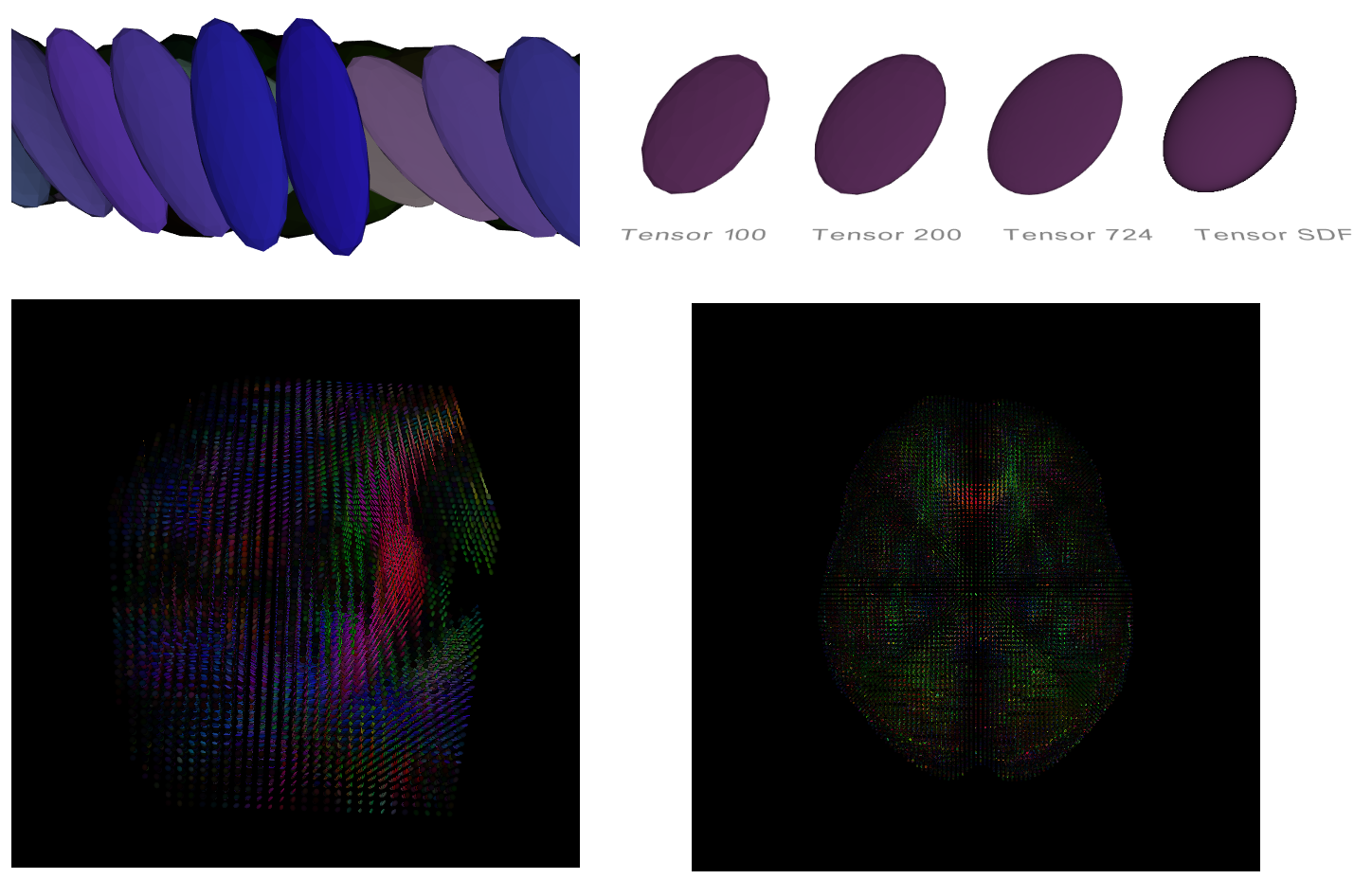
A first approach for tensor glyph generation has been made, using ray marching and SDF applied to a box. The current implementation (tensor_slicer) requires a sphere with a specific number of vertices to be deformed. Based on this model, a sphere with more vertices is needed to get a higher resolution. Because the ray marching technique does not use polygonal meshes, it is possible to define perfectly smooth surfaces and still obtain a fast rendering.
Details of the implementation:
- Vertex shader pre-calculations: Some minor calculations are done in the vertex shader. One, corresponding to the eigenvalues constraining and min-max normalization, are to avoid incorrect visualizations when the difference between the eigenvalues is too large. And the other is related to the tensor matrix calculation given by the diffusion tensor definition T=R-1ΛR, where R is a rotation matrix that transforms the standard basis onto the eigenvector basis, and Λ is the diagonal matrix of eigenvalues [4].
- Ellipsoid SDF definition: The definition of the SDF is done in the fragment shader inside the
mapfunction, which is used later for the ray marching algorithm and the normals calculation. We define the SDF more simply by transforming a sphere into an ellipsoid, considering that the SDF of a sphere is easily computed and the definition of a tensor gives us a linear transformation of a given geometry. Also, as scaling is not a rigid body transformation, we multiply the final result by a factor to compensate for the difference, which gave us the SDF of the ellipsoid defined assdSphere(tensorMatrix * (position - centerMCVSOutput), scaleVSOutput*0.48) * scFactor. - Ray marching algorithm and lighting: For the ray marching algorithm, a small value of 20 was taken as the maximum distance since we apply the technique to each individual object and not all at the same time. Additionally, we set the convergence precision to 0.001. We use the central differences method to compute the normals necessary for the scene’s illumination, besides the Blinn-Phong lighting technique, which is high-quality and computationally cheap.
- Visualization example: Below is a detailed visualization of the ellipsoids created from this new implementation.
This implementation does show a better quality in the displayed glyphs, and supports the display of a large amount of data, as seen in the image below. For this reason, a tutorial was made to justify in more detail the value of this new implementation. Below are some images generated for the tutorial.
Pull Requests:
- Ellipsoid actor implemented with SDF (Merged) fury-gl/fury#791
- Tutorial on using ellipsoid actor to visualize tensor ellipsoids for DTI (Merged) fury-gl/fury#818
Future work: In line with one of the initial objectives, it is expected to implement billboards later on to improve the performance, i.e., higher frame rate and less memory usage for the tensor ellipsoid creation. In addition to looking for ways to optimize the naive ray marching algorithm and the definition of SDFs.
Objectives in Progress
-
DTI uncertainty visualization
The DTI visualization pipeline is fairly complex, as a level of uncertainty arises, which, if visualized, helps to assess the model's accuracy. This measure is not currently implemented, and even though there are several methods to calculate and visualize the uncertainty in the DTI model, because of its simplicity and visual representation, we considered Matrix Perturbation Analysis (MPA) proposed by Basser [1]. This measurement is visualized as double cones representing the variance of the main direction of diffusion, for which the ray marching technique was also used to create these objects.
Details of the implementation:
- Source of uncertainty: The method of MPA arises from the susceptibility of DTI to dMRI noise present in diffusion-weighted images (DWIs), and also because the model is inherently statistical, making the tensor estimation and other derived quantities to be random variables [1]. For this reason, this method focus on the premise that image noise produces a random perturbation in the diffusion tensor estimation, and therefore in the calculation of eigenvalues and eigenvectors, particularly in the first eigenvector associated with the main diffusion direction.
- Mathematical equation: The description of the perturbation of the principal eigenvector is given by math formula where ΔD corresponds to the estimated perturbation matrix of D given by the diagonal elements of the covariance matrix Σa≈(BTΣe-1B)-1, where Σe is the covariance matrix of the error e, defined as a diagonal matrix made with the diagonal elements of (Σe-1)=⟨S(b)⟩2/ση2 . Then, to get the angle θ between the perturbed principal eigenvector of D, ε1+Δε1, and the estimated eigenvector ε1, can be approximated by θ =tan-1(|Δε1|) [2]. Taking into account the above, we define the function
main_dir_uncertainty(evals, evecs, signal, sigma, b_matrix)that calculates the uncertainty of the eigenvector associated to the main direction of diffusion. - Double cone SDF definition: The final SDF is composed by the union of 2 separately cones using the definition taken from this list of distance functions, in this way we have the SDF for the double cone defined as
opUnion(sdCone(p,a,h), sdCone(-p,a,h)) * scaleVSOutput - Visualization example: Below is a demo of how this new feature is intended to be used, an image of diffusion tensor ellipsoids and their associated uncertainty cones.
The implementation is almost complete, but as it is a new addition that includes mathematical calculations and for which there is no direct reference for comparison, it requires a more detail review before it can be incorporated.
Pull Request:
- DTI uncertainty visualization (Under Review) fury-gl/fury#810
Future work: A tutorial will be made explaining in more detail how to calculate the parameters needed for the uncertainty cones using dipy functions, specifically: estimate_sigma for the noise variance calculation, design_matrix to get the b-matrix, and tensor_prediction for the signal estimation. Additionally, when ODF implementation is complete, uncertainty for this other reconstruction model is expected to be added, using semitransparent glyphs representing the mean directional information proposed by Tournier [3].
-
ODF actor implemented with SDF
HARDI-based techniques require more images than DTI, however, they model the diffusion directions as probability distribution functions (PDFs), and the fitted values are returned as orientation distribution functions (ODFs). ODFs are more diffusion sensitive than the diffusion tensor and, therefore, can determine the structure of multi-directional voxels very common in the white matter regions of the brain [3]. The current actor to display this kind of glyphs is the odf_slicer which, given an array of spherical harmonics (SH) coefficients renders a grid of ODFs, which are created from a sphere with a specific number of vertices that fit the data.
For the application of this model using the same SDF ray marching techniques, we need the data of the SH coefficients, which are used to calculate the orientation distribution function (ODF) described here. Different SH bases can be used, but for this first approach we focus on descoteaux07 (as labeled in dipy). After performing the necessary calculations, we obtain an approximate result of the current implementation of FURY, as seen below.
With a first implementation we start to solve some issues related to direction, color, and data handling, to obtain exactly the same results as the current implementation.
Details on the issues:
- The direction and the scaling: When the shape of the ODF is more sphere-like, the size of the glyph is smaller, so for the moment it needs to be adjusted manually, but the idea is to find a relationship between the coefficients and the final object size so it can be automatically scaled. Additionally, as seen in the image, the direction does not match. To fix this, an adjustment in the calculation of the spherical coordinates can be made, or pass the direction information directly.
- Pass the coefficients data efficiently: I'm currently creating one actor per glyph since I'm using a uniform array to pass the coefficients, but the idea is to pass all the data simultaneously. The first idea is to encode the coefficients data through a texture and retrieve them in the fragment shader.
- The colormapping and the lighting: As these objects present curvatures with quite a bit of detail in some cases, this requires more specific lighting work, in addition to having now not only one color but a color map. This can also be done with texture, but it is necessary to see in more detail how to adjust the texture to the glyph's shape.
More details on current progress can be seen in blogpost of week 11 and week 12.
Working branch:
- ODF implementation (Under Development) https://github.com/tvcastillod/fury/tree/SH-for-ODF-impl
GSoC Weekly Blogs
My blog posts can be found on the FURY website and the Python GSoC blog.
Timeline
| Date | Description | Blog Link |
|---|---|---|
| Week 0 (02-06-2022) |
Community Bounding Period | FURY - Python |
| Week 1 (05-06-2022) |
Ellipsoid actor implemented with SDF | FURY - Python |
| Week 2 (12-06-2022) |
Making adjustments to the Ellipsoid Actor | FURY - Python |
| Week 3 (19-06-2022) |
Working on uncertainty and details of the first PR | FURY - Python |
| Week 4 (27-06-2022) |
First draft of the DTI uncertainty visualization | FURY - Python |
| Week 5 (03-07-2022) |
Preparing the data for the Ellipsoid tutorial | FURY - Python |
| Week 6 (10-07-2022) |
First draft of the Ellipsoid tutorial | FURY - Python |
| Week 7 (17-07-2022) |
Adjustments on the Uncertainty Cones visualization | FURY - Python |
| Week 8 (25-07-2022) |
Working on Ellipsoid Tutorial and exploring SH | FURY - Python |
| Week 9 (31-07-2022) |
Tutorial done and polishing DTI uncertainty | FURY - Python |
| Week 10 (08-08-2022) |
Start of SH implementation experiments | FURY - Python |
| Week 11 (16-08-2022) |
Adjusting ODF implementation and looking for solutions on issues found | FURY - Python |
| Week 12 (24-08-2022) |
Experimenting with ODFs implementation | FURY - Python |
References
[1] Basser, P. J. (1997). Quantifying errors in fiber direction and diffusion tensor field maps resulting from MR noise. In 5th Scientific Meeting of the ISMRM (Vol. 1740).
[2] Chang, L. C., Koay, C. G., Pierpaoli, C., & Basser, P. J. (2007). Variance of estimated DTI‐derived parameters via first‐order perturbation methods. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 57(1), 141-149.
[3] J-Donald Tournier, Fernando Calamante, David G Gadian, and Alan Connelly. Direct estimation of the fiber orientation density function from diffusion-weighted mri data using spherical deconvolution. Neuroimage, 23(3):1176–1185, 2004.
[4] Gordon Kindlmann. Superquadric tensor glyphs. In Proceedings of the Sixth Joint Eurographics-IEEE TCVG conference on Visualization, pages 147–154, 2004.